红黑树插入和删除结点的全程演示
作者:July、saturnman。 时间:二零一一年三月二十八日。 出处:。 声明:版权所有,侵权必究。 -----------------------------------
引言:
目前国内图书市场上,抑或网上讲解红黑树的资料层次不齐,混乱不清,没有一个完整而统一的阐述。而本人的红黑树系列四篇文章(详见文末的参考文献),虽然从头至尾,讲的有根有据,层次清晰,然距离读者真正做到红黑树了然于胸,则还缺点什么。
而我们知道,即便在经典的导论一书上,也没有把所有的插入、删除情况一一道尽,直接导致了不少读者的迷惑,而我的红黑树系列第4篇文章:,虽然早已把所有的插入、删除情况都一一道尽了,但也缺了点东西。
缺点什么东西列?对了,缺的就是一个完完整整的,包含所有插入、删除情况全部过程的全程演示图,即缺一个例子,缺一个完整的图来从头至尾阐述这一切。
ok,本文,即以40幅图来全程演示此红黑树的所有插入,和删除情况。相信,一定会对您理解红黑树有所帮助。
话不絮烦,下面,本文便以此篇文章:一步一图一代码,一定要让你真正彻底明白红黑树为纲,从插入一个结点到最后插入全部结点,再到后来一个一个把结点全部删除的情况一一阐述。
由于为了有个完整统一,红黑树插入和删除情况在此合作成一篇文章。同时,由于本人的红黑树系列的四篇文章已经把红黑树的插入、删除情况都一一详尽的阐述过了,因此,有关红黑树的原理,本文不再赘述,只侧重于用图来一一全程演示结点的插入和删除情况。有任何问题,欢迎指正。
红黑树插入情况全过程演示
通过本人的红黑树系列第4篇文章,我们已经知道,红黑树的所有插入情况有以下五种:
情形1: 新节点N位于树的根上,没有父节点
情形2: 新节点的父节点P是黑色情形3:父节点P、叔叔节点U,都为红色,[对应第二篇文章中,的情况1:z的叔叔是红色的。]情形4: 父节点P是红色,叔叔节点U是黑色或NIL; 插入节点N是其父节点P的右孩子,而父节点P又是其父节点的左孩子。[对应我第二篇文章中,的情况2:z的叔叔是黑色的,且z是右孩子]情形5: 父节点P是红色,而叔父节点U 是黑色或NIL, 要插入的节点N 是其父节点的左孩子,而父节点P又是其父G的左孩子。[对应我第二篇文章中,情况3:z的叔叔是黑色的,且z是左孩子。]详细,可参考此红黑树系列第4篇文章:。
首先,各个结点插入与以上的各种插入情况,一一对应起来,如图: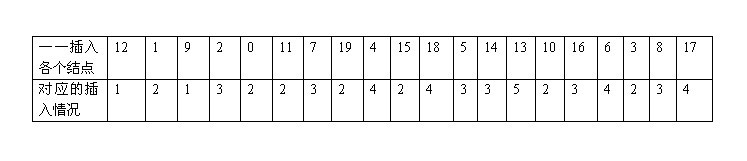
以下的20张图,是依次插入这些结点:12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17的全程演示图,已经把所有的5种插入情况,都全部涉及到了:

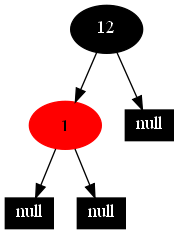

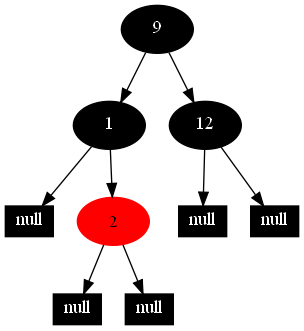
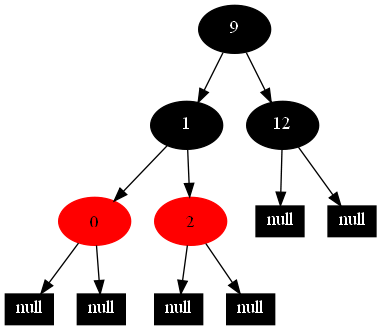

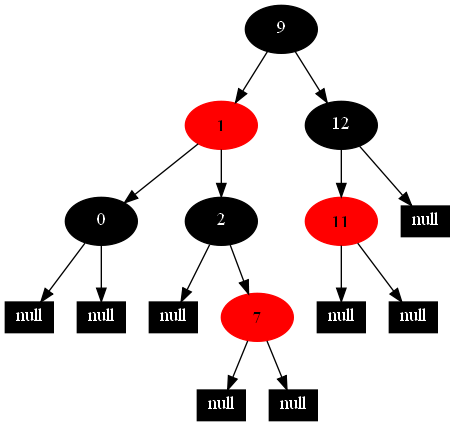
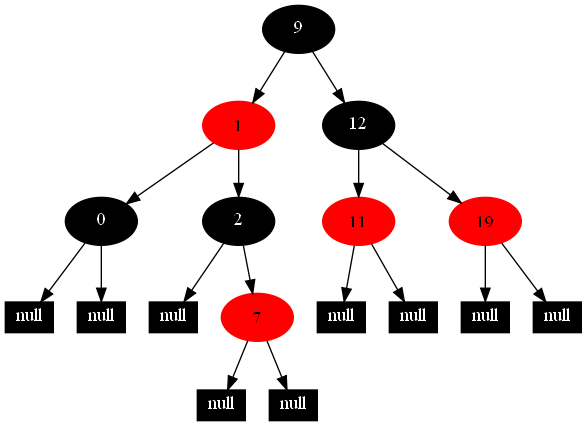
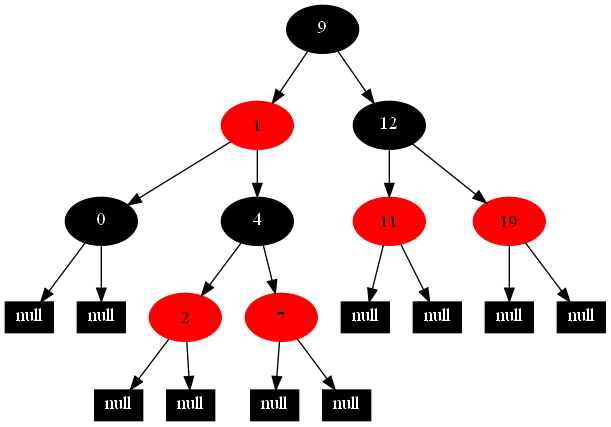
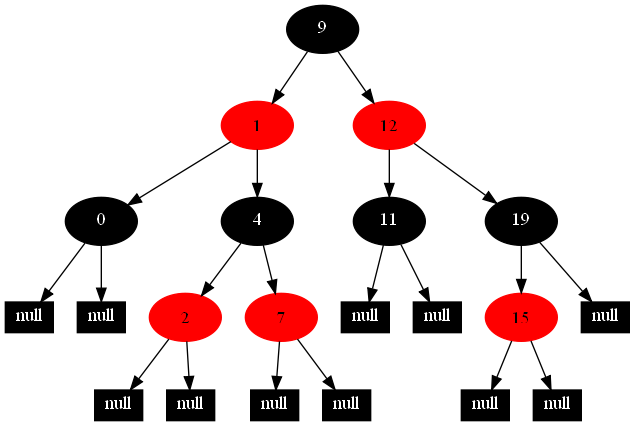
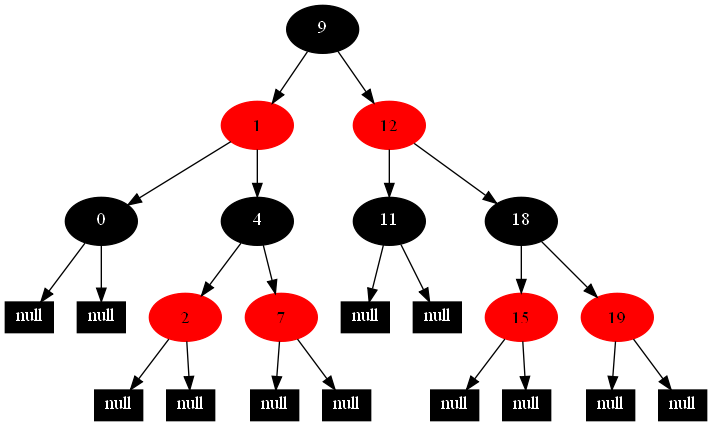
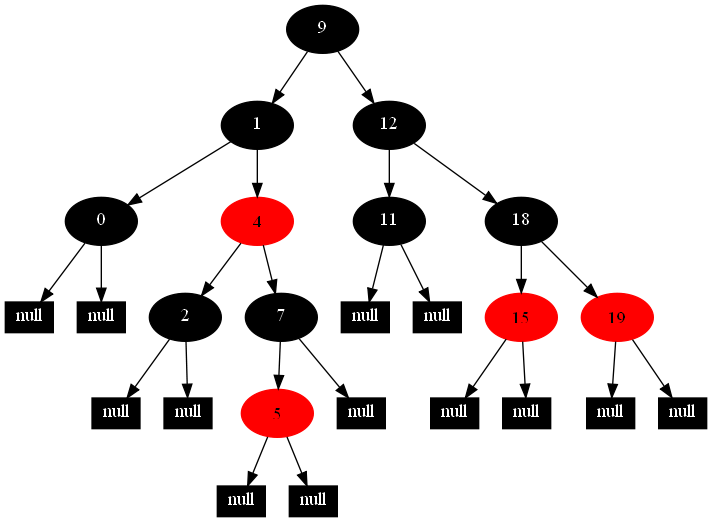
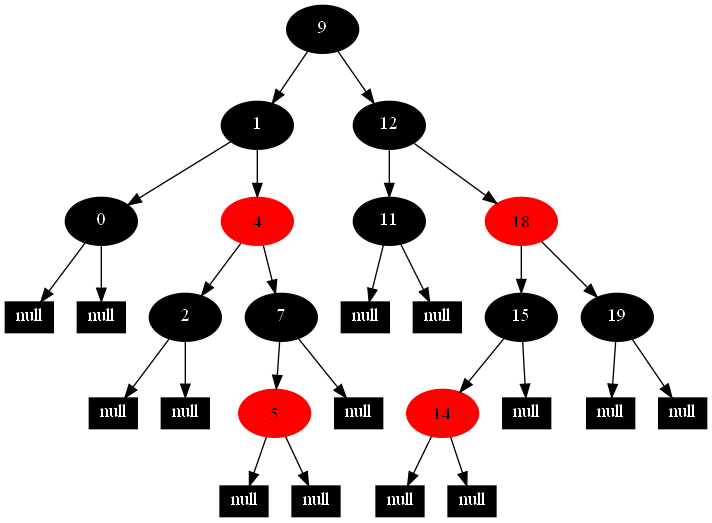
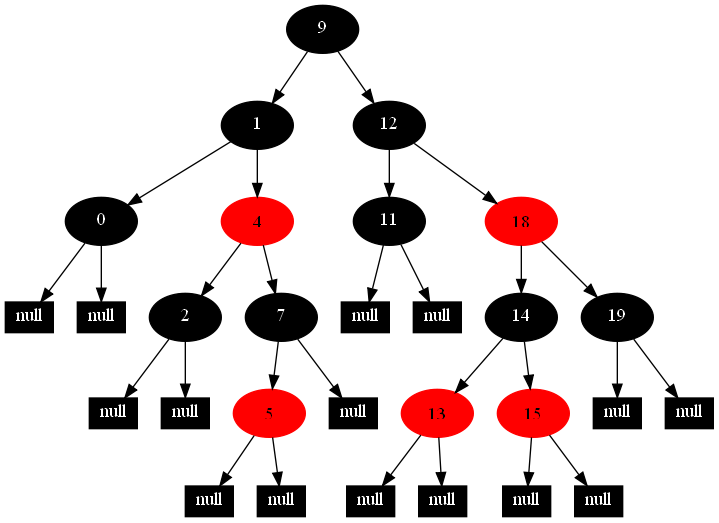
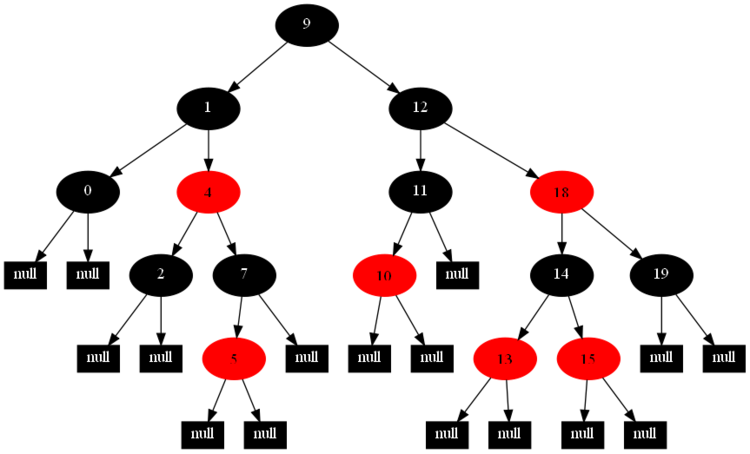
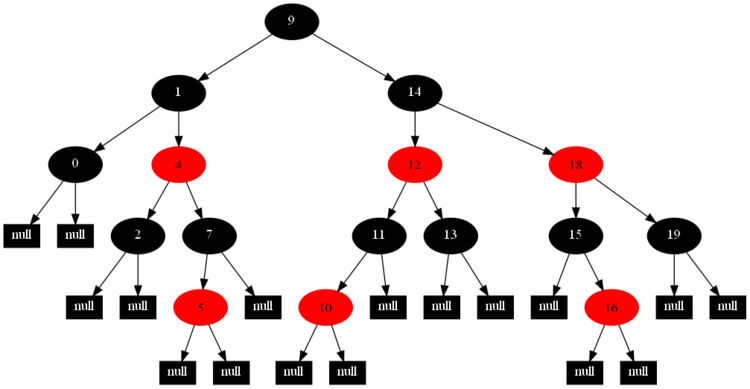
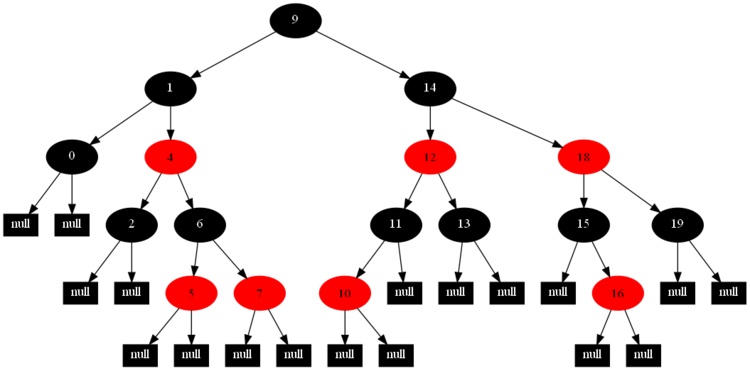
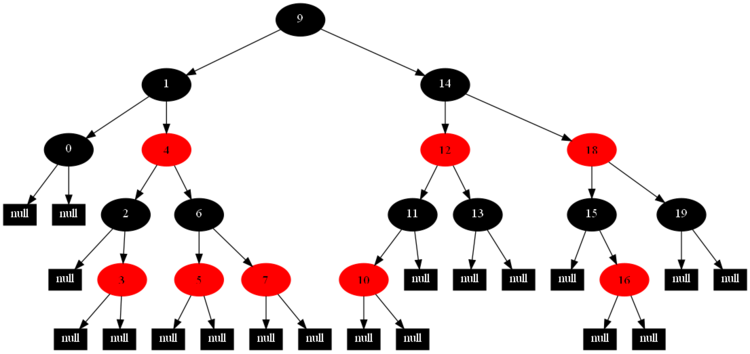
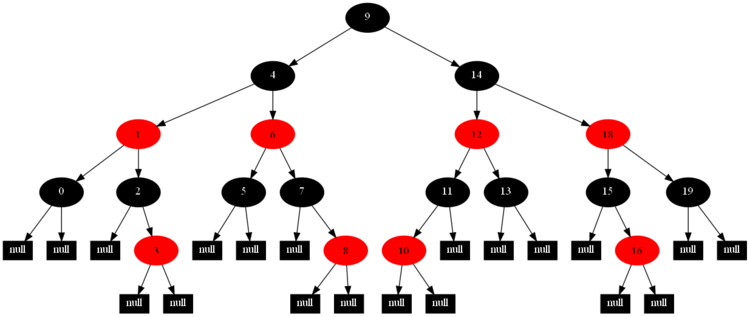
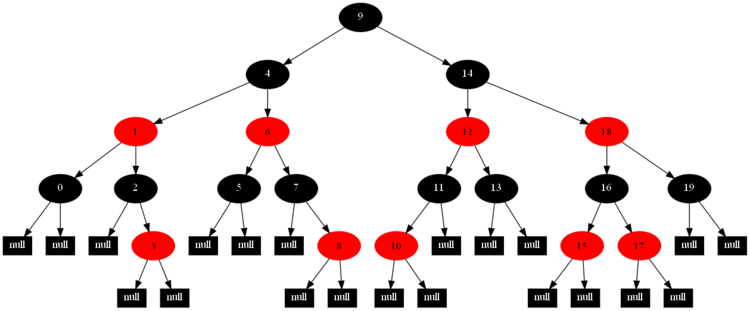
红黑树的一一插入各结点:12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17的全程演示图完。
红黑树删除情况全过程演示 红黑树的所有删除情况,如下:
情况1: N 是新的根。
情形2:兄弟节点S是红色[对应我第二篇文章中,情况1:x的兄弟w是红色的。]情况 3: 兄弟节点S是黑色的,且S的俩个儿子都是黑色的。但N的父节点P,是黑色。[对应我第二篇文章中,情况2:x的兄弟w是黑色的,且兄弟w的俩个儿子都是黑色的。(这里,N的父节点P为黑)]情况4: 兄弟节点S 是黑色的、S 的儿子也都是黑色的,但是 N 的父亲P,是红色。 [还是对应我第二篇文章中,情况2:x的兄弟w是黑色的,且w的俩个孩子都是黑色的。 (这里,N的父节点P为红)]情况5: 兄弟S为黑色,S 的左儿子是红色,S 的右儿子是黑色,而N是它父亲的左儿子。 //此种情况,最后转化到下面的情况6。[对应我第二篇文章中,情况3:x的兄弟w是黑色的,w的左孩子是红色,w的右孩子是黑色。]情况6: 兄弟节点S是黑色,S的右儿子是红色,而 N 是它父亲的左儿子。[对应我第二篇文章中,情况4:x的兄弟w是黑色的,且w的右孩子时红色的。]接下来,便是一一删除这些点12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17为例,即,红黑树删除情况全程演示:
各个结点删除与以上的六种情况,一一对应起来,如图: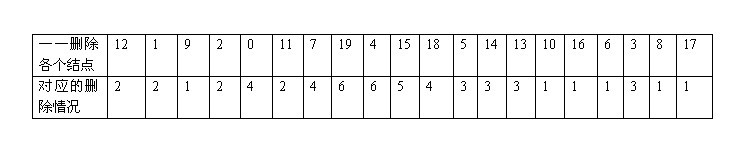
首先,插入12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17结点后,形成的红黑树为:
然后,以下的20张图,是一一删除这些结点12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17所得到的删除情况的全程演示图:
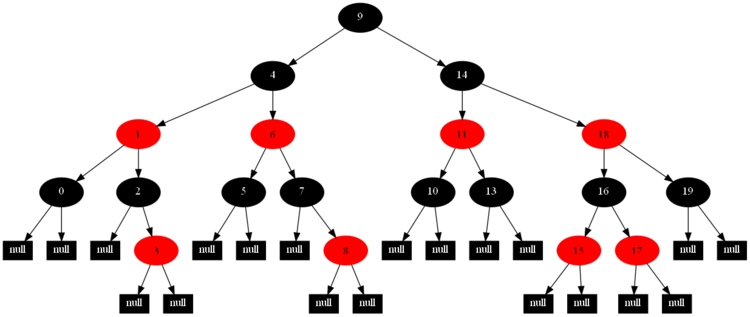
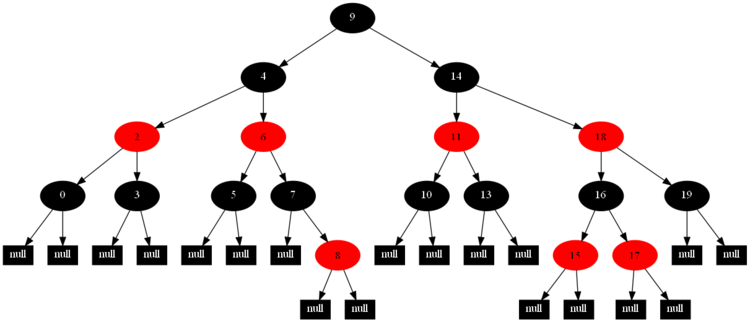
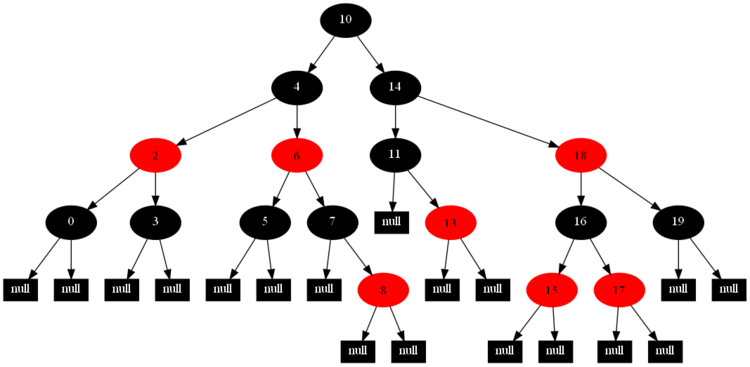
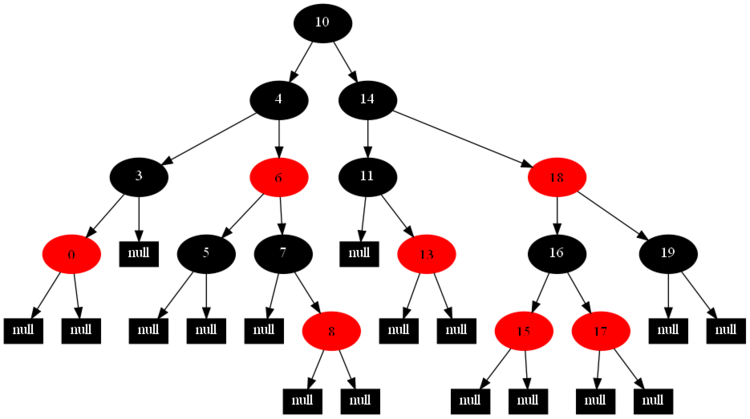

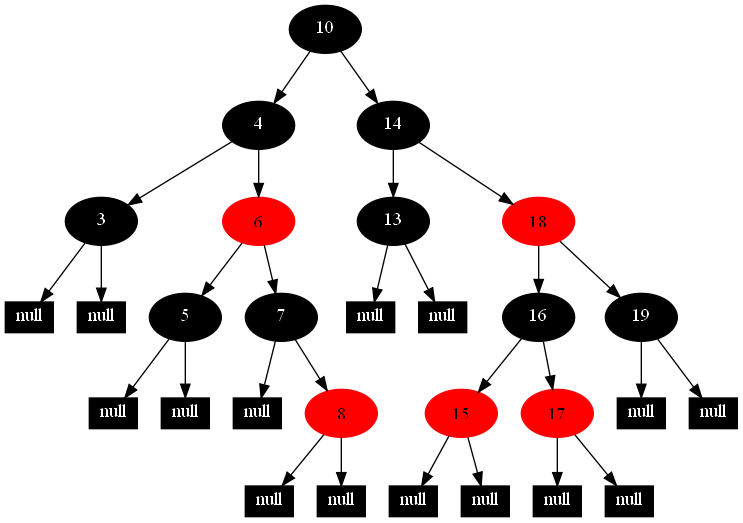
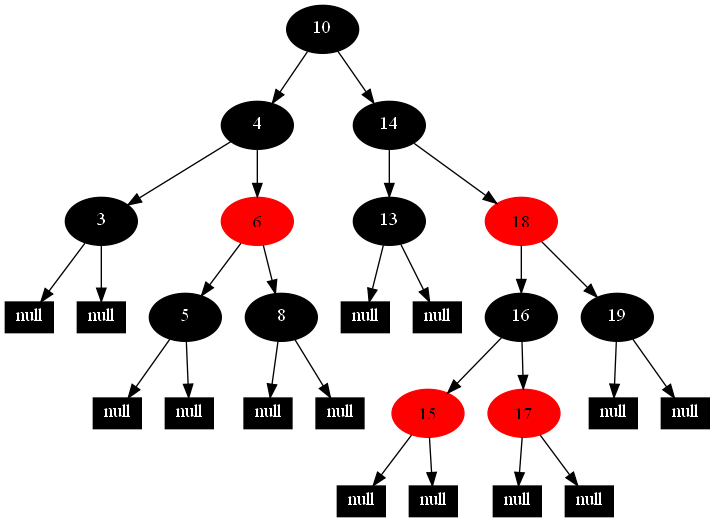
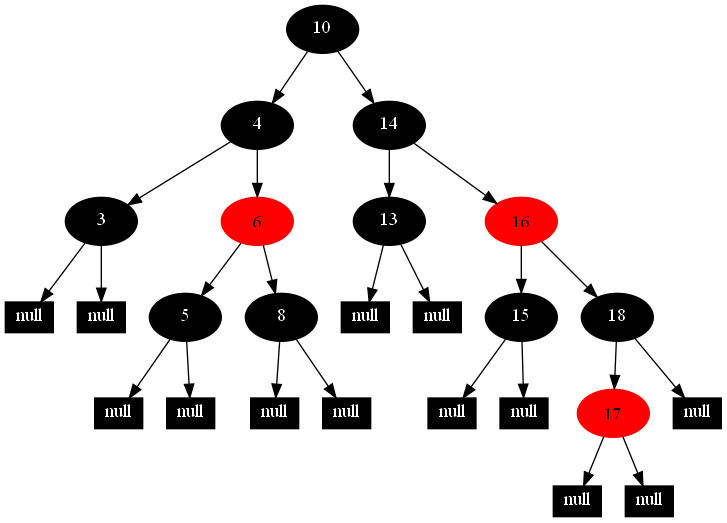

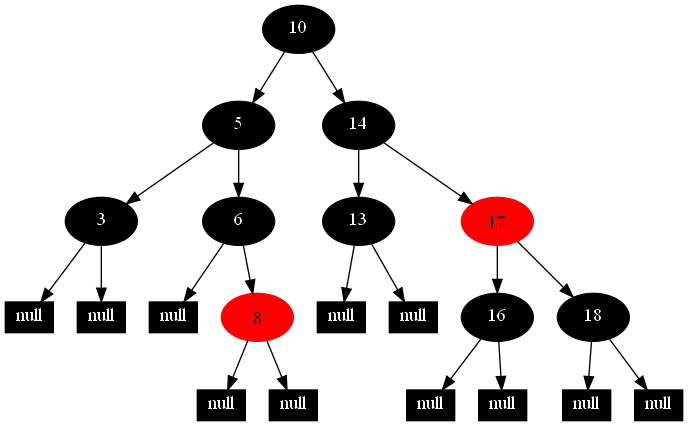

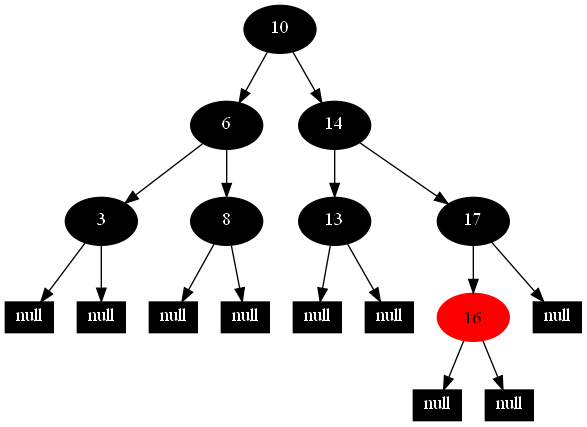
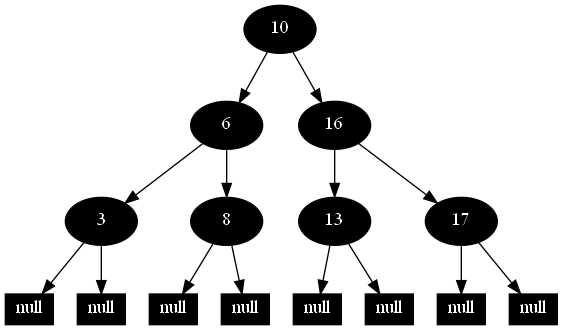
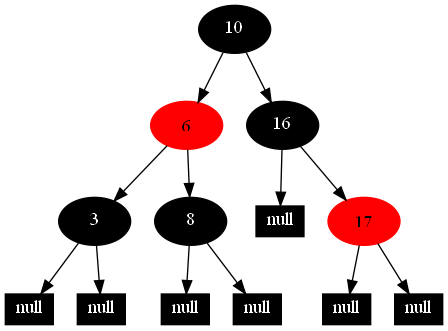
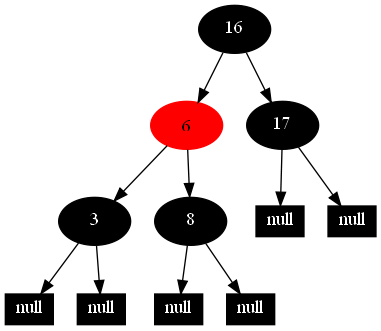

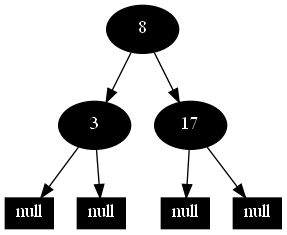
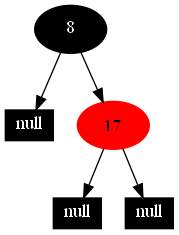

![]()
红黑树的一一删除各结点:12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17的全程演示图完。
参考文献,本人代表作之一:红黑树系列:
7、 。全文完。